İrəli Data Science. Numpy ilə simulasiyalar

Tarixən eksperimentlər və simulasiyalar nəzəriyyələrin formalaşmasında və onların yoxlanılmasında böyük rola sahib olublar. Onların köməyi ilə biz:

• nəzəriyyənin elmiliyini yoxlaya bilərik. Popper kriteriyasına görə, istənilən empirik sistemin eksperimental yolla təkzibedilmə xüsusiyyəti olmalıdır.
• nəzəriyyələrin həqiqiliyinin təsdiq edə bilərik. Buna elmi dildə verifikasiya deyilir.

Data science üçün də simulasiyaların rolu olduqca böyükdür. Əsasən də müəllimli öyrətmə (supervised learning) zamanı simulasiyalar ilə verilənlərdə olan çatışmazlıqları görə, tənzimləyə, və ya datanın az olduğu sahələrdə onu süni yolla artıraraq aradan qaldıra bilərsiniz.

Bu dəfəki məqaləmdə klassik zər atımını Python ilə simulyasiya edib nəticələri analiz edəcəyik.

Tutaq ki, bizə 8 üzlü iki zər verilib. Hər iki zərin üzlərini 1-8 aralığında rəqəmləyək. Hər dəfə zəri atanda hansı rəqəm düşürsə, o qədər də xal qazanaq. Məsələ odur ki, o zərlərin hər birini ayrı insan düzəldib. Nəticə olaraq, onlar bir-biri ilə eyni deyillər və hər hansı bir üzlərinin düşmə ehtimalı fərqlidir. Lakin, biz o ehtimalları bilirik. A və B adlı şəxslərin hərəsinə bir zər verək. Sizcə kim ilk olaraq 100 xal yığar? Daha maraqlı sual: Hansı zər neçə gedişə 100 xal yığar?

İndi isə məsələni Pythonda həll edək. Planımız isə belə olacaq:

• Hər iki zər üçün ehtimalları yaradaq. Bunu da Pythonda edə bilərik, əl ilə yazmağa gərək yoxdur.
• Hər iki zəri 100 dəfə ataq. Çünki, nəticədən asılı olmayaraq, hər dəfəsində azı 1 xal qazanarıq və 100 dəfə atsaq azı 100 xal qazanarıq.
• Bu eksperimenti 1k (min) dəfə təkrar edirik. Böyük rəqəmlər nəzəriyyəsinə görə, nə qədər çox təkrar etsək, nəticələr həqiqi nəticəyə bir o qədər yaxın olacaq. Bizə isə 1k dəfə artıqlaması ilə bəsdir.
• Oyunları vizuallaşdıraq. Vizuallaşdırma ümumiləşdirici xarajter daşıyacaq.

İlk öncə, alətlərimizi import edək. Bizə NumPy, Seaborn lazım olacaq.

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

İndi isə ehtimalları generasiya edək. Bunun üçün ən rahat yol Dirişle paylanmasından təsadüfi seçimlər etməkdir. np.random.dirichlet funksiyasını istifadə edəcəyik. Bu funksiya bizə cəmi 1-ə bərabər olan 8 rəqəmdən ibarət vektorlar verəcək. Bizə isə iki vektor lazımdır.

probs_1, probs_2 = np.random.dirichlet(np.ones(8),
                                        size=2) # ehtimallar
sides = np.arange(1, 9) # xallar

np.random.choice funksiyası ilə də, verilmiş xallardan verilmiş ehtimal ilə (bax yuxarı) seçimlər edə bilərik. Size arqumenti bizə bütün simulyasiyanı birdəfəyə etmək imkanı verir. 1k sətir oyunların sayını, 100 sütun isə hər oyun zamanı atışların sayını göstərir. Nəticədə biz 1-8 aralığında olan 1000 x 100 matris əldə edəcəyik.

np.random.choice(sides, size = (1000, 100), p = probs_1)

Daha sonra isə biz həmin matrisin sətir üzərində kumlyativ cəmini tapacağıq. Çünki, bizə maraqlı olan o xalların cəmidir ki, daha sonra biz o cəmin 100-ə bərabərliyini yoxlaya bilək.

die_1_results = np.random.choice(sides, 
                                size = (1000, 100), 
                                p = probs_1).cumsum(axis = 1)
die_2_results = np.random.choice(sides, 
                                size = (1000, 100), 
                                p = probs_2).cumsum(axis = 1)

Xalların cəmi 100-ə bərabər olanda oyun bitdiyi üçün, biz hər bir zərin neçə gedişə 100 xal yığdığını tapmalıyıq. Bunun üçün bizə np.argmax lazımdır. O verilmiş vektorun və ya matrisin verilmiş şərti ilk ödəyən elementinin indeksini bizə verəcək.

die_1_won_the_game_at = np.argmax(die_1_results >= 100, axis = 1)

die_2_won_the_game_at = np.argmax(die_2_results >= 100, axis = 1)

İndi isə, hər bir zərin neçə dəfə qalib olduğunu tapaq. Bunun üçün bizə ` die_1_won_the_game_at və die_2_won_the_game_at obyektlərini qarşılıqlı müqayisə etmək lazımdır. Adi matris müqayisəsi bunu rahatlıqla etməyə imkan verir. Sonda isə, np.sum ilə qalibiyyətlərin sayını tapacağıq.

die_1_won = np.sum(die_1_won_the_game_at < die_2_won_the_game_at)

die_2_won = np.sum(die_2_won_the_game_at < die_1_won_the_game_at)

tie_game_count = np.sum(die_1_won_the_game_at == die_2_won_the_game_at)

İndi isə gəlin bunların hamısını bir funksiya daxilinə salıb həm də vizuallaşdıraq.

   
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

def run_experiment(game_rounds = 1000, throw_count_per_round = 100):
    probs_1, probs_2 = np.random.dirichlet(np.ones(8),
                                        size=2)
    sides = np.arange(1, 9)

    die_1_results = np.random.choice(sides, size = (game_rounds,      throw_count_per_round), p = probs_1).cumsum(axis = 1)
    die_2_results = np.random.choice(sides, size = (game_rounds, throw_count_per_round), p = probs_2).cumsum(axis = 1)
    
    die_1_got_100_at = np.argmax(die_1_results >= 100, axis = 1)
    die_2_got_100_at = np.argmax(die_2_results >= 100, axis = 1)
    
    die_1_won = np.sum(die_1_got_100_at < die_2_got_100_at)
    die_2_won = np.sum(die_2_got_100_at < die_1_got_100_at)
    tie_game_count = np.sum(die_1_got_100_at == die_2_got_100_at)
    
    print(f"Die 1 won {die_1_won} times")
    print(f"Die 2 won {die_2_won} times")
    print(f"Tie game happened {tie_game_count} times")
    
    ax1 = sns.distplot(die_1_got_100_at, color= "red")
    ax2 = sns.distplot(die_2_got_100_at, color = "green")
    plt.show()

run_experiment()

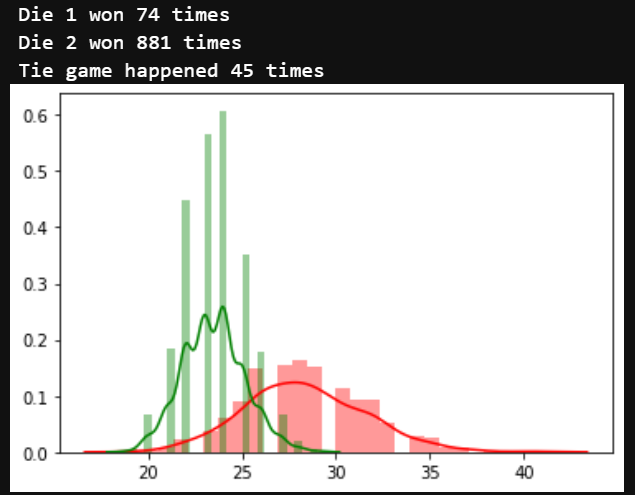
Nəticədə biz belə bir şəkil alacağıq. Sizdə fərqli şəkil alına bilər. Çünki eksperiment təsadüfi xarakter daşıyır. Və üzlərin düşmə ehtimalları fərqli olacaq.

Nəticədən görünür ki, yaşıl xəttin ifadə etdiyi ikinci zərə ortalama 23 atış lazım olub ki, o 100 xal yığsın. Halbuki, qırmızı xəttin ifadə etdiyi birinci zər üçün bu rəqəm 27 olub.